Mental Factors of No Importance

There are few things I enjoy more in a scientific document than a particularly punchy patch of purple prose. In 1939, Truman Kelley had an important insight to share, and I love it that he got his point across by going all in and over the top:

The first earmark of an unimportant factor is its Venus-like birth from the meditations of a Spranger, the libido of a Freud, the hunch of an enthusiastic employment officer, or the dial of a differential analyzer. The second earmark is also Venus-like—the factor stands in virgin purity, untrammeled by clothes of doubt, untouched by considerations of probable error, unqualified by tentative endorsement. The third earmark is almost a consequent of the other two—the factor has never been put to work, it has never served the needs of man in school, in business, in social adaptation. Truly none of these earmarks detract from the beauty of the picture and possibly this Venus will scrub floors as well as win acclaim for harmony of proportion and then, indeed, we shall be blessed. But initially let us call a factor with these earmarks just a Venus-factor and not load it down or trust it with heavy work.

What is the heavy work that is to be done? We have eight million unemployed, another many millions feeling thwarted and believing that could they but find a channel of expression more fitted to their talents, their life would be richer and society of which they are a part would be the better. The heavy work resting squarely upon the shoulders of the typologist, of the mental factorist, of the character analyst, and upon the comprehensiveness, accuracy, and analytical nature of the mental measures that he uses, is to render aid in the mental and social adjustments necessary to alleviate the thwartings mentioned.

This heavy work must not be encumbered with trivial mental factors. Let me suggest a Factor-of-no-importance that might be derived by the method of statistical analysis of test data. If tests of taste sensitivity to para-ethoxy-phenol-thio-carbamide were included in a series of tests to be factorized by matrix methods I have no doubt that a taste trait would evolve as an independent factor. Certainly it is real, psychologically real, perhaps genetically real, but still in comparison with those mental, sensory, and motor things that underlie the adequate adjustment of individuals in the society in which we live it certainly is a Factor-of-no-importance. I can, by a vigorous stretch of the imagination, conceive of a society in which such a factor would be important. I do not object to students spending their time upon such factors with the hope of discovering something of genetic or other importance, but I do insist that evidence of existence of a factor be not cited as evidence that it is important in the meeting of pressing guidance and social problems. (pp. 140–141)

Kelley, T. L. (1939). Mental factors of no importance. Journal of Educational Psychology, 30(2), 139–142. https://doi.org/10.1037/h0056336

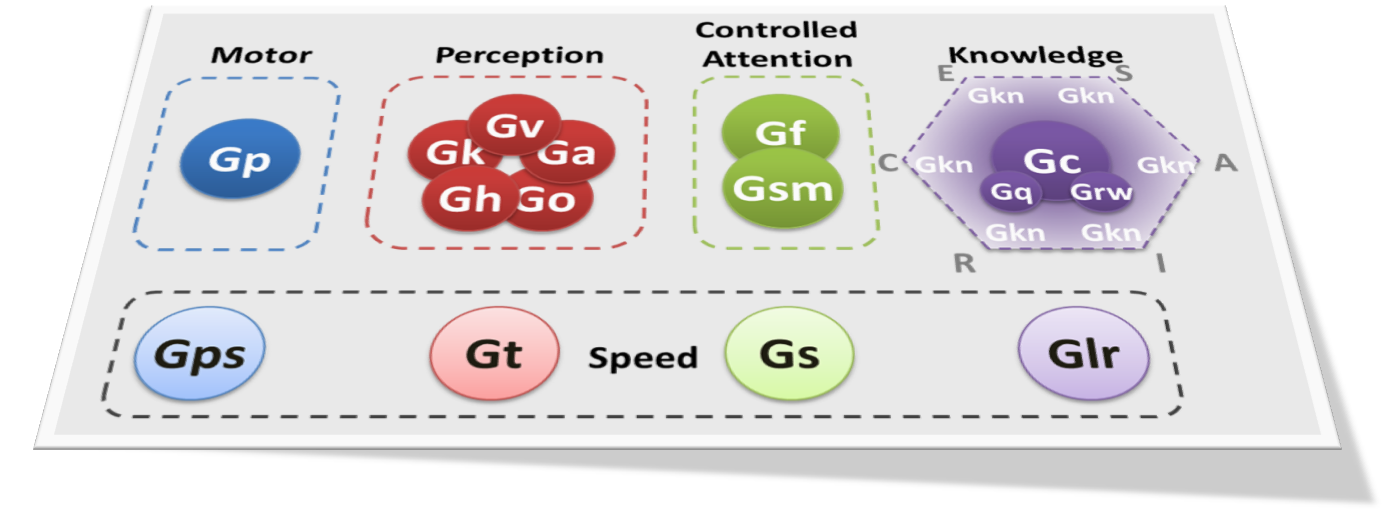
In his 1993 masterwork, Human Cognitive Abilities, A Survey of Factor-Analytic Studies, John Carroll occasionally noted that some of the factors he identified had no known utility at the time of writing. To prevent endless proliferation of useless ability constructs, Kevin McGrew and I (Schneider & McGrew, 2018) proposed that new ability constructs should meet the following criteria:

1. The content domain of a new ability must be laid out clearly.
2. The new ability must be measurable with performance tests using multiple test paradigms.
3. Measures of the new ability must demonstrate convergent and discriminant validity when measured alongside other abilities.
4. Measures of the new ability must demonstrate incremental validity over measures of other more established abilities when predicting important outcomes.
5. The new ability construct should be linked plausibly to specific neurological functions.
6. The new ability construct should be linked plausibly to functions that evolved to help humans survive and reproduce.

These criteria were inspired by similar proposals by Raymond Cattell, Howard Gardner, and John Mayer and his colleagues.

A systematic and thorough review of the evidence of each ability construct in CHC theory is sorely needed. Some of the broad CHC abilities have been vetted thoroughly enough such that they clearly meet all these criteria, but others have not. Most narrow abilities have long languished in the preliminary stages of construct validation. So much work to do…

Defining Intelligence: “It’s a trap!”

It is a favourite debating ploy in discussions about human intelligence to ask for a definition of the construct. One meaning of ‘define’ in the Oxford English Dictionary is ‘give the exact meaning of’. If differential psychologists are daft enough to attempt this, they will find they have been tricked into delivering a hostage to fortune, the premature issue will be rent by inquisitors. (p. 1)

Deary, I.J. (2000). Looking down on human intelligence: From psychometrics to the brain. Oxford University Press.

Deary advises intelligence researchers to instead try to mark the boundaries of the concept of intelligence. Some scholars in other disciplines also have ambivalent relationships with exact definitions. Mike Brown, who discovered several “dwarf planets” and many other large objects in our solar system beyond Pluto, explained why he does not take seriously the International Astronomical Union’s official definition of the term planet that excluded Pluto:

In the entire field of astronomy, there is no word other than planet that has a precise, lawyerly definition, in which certain criteria are specifically enumerated. Why does planet have such a definition but star, galaxy, and giant molecular cloud do not? Because in astronomy, as in most sciences, scientists work by concepts rather than by definitions. The concept of a star is clear; a star is a collection of gas with fusion reactions in the interior giving off energy. A galaxy is a large, bound collection of stars. A giant molecular cloud is a giant cloud of molecules. The concept of a planet—in the eight-planet solar system—is equally simple to state. A planet is a one of a small number of bodies that dominate a planetary system. That is a concept, not a definition. How would you write that down in a precise definition?
I wouldn’t. Once you write down a definition with lawyerly precision, you get the lawyers involved in deciding whether or not your objects are planets. Astronomers work in concepts. We rarely call in the attorneys for adjudication. (p. 242)

Brown, M. (2012). How I killed Pluto and why it had it coming. Spiegel & Grau.

Assessment Report Template

Today at NASP 2019, I gave two workshops on psychological assessment report writing. Here are links to two complete reports:

Liam

Renaldo

Caveat Observator: On the Seductive Validity of Behavioral Observations

Seeing is believing, but first impressions do not tell the whole truth.

Well, who you gonna believe, me or your own eyes?

Chico Marx in Duck Soup (1933)

The sirens of observed behavior do not seduce us to a watery grave; they sing of truths so satisfying that we cease to sail. At port, we tell tales of whole oceans after having seen a single cove just outside the harbor.

It might seem like direct observation would be the final authority that trumps all other forms of evidence. However, there are reliability and validity concerns about direct observation that are every bit as serious as those associated with ability tests, rating scales, and interviews (Meier, 1994). It is not that observed behavior gives false information, but the true information it provides is so vivid that other truths are ignored, and our interpretation is incomplete.

Even though we know that behavior can vary considerably from day to day, it is rare for examiners to observe examinees for more than an hour or two in naturalistic settings (e.g., classrooms, playgrounds, and group homes). Worse, most direct observation occurs in the unnaturalistic setting of the testing environment. The testing environment pulls for particular sets of temporary behaviors that are easily mistaken for persistent personality traits. Even those of us who intellectually appreciate the allure of the fundamental attribution error (Ross, 1977) find it hard to resist the urge to overgeneralize that which we have observed with our own eyes.

We have reason to reserve judgment when an examinee does something unusual in the testing environment because the testing environment is itself unusual. The testing environment differs from most other environments, in part because the interaction is most often one-to-one and thus more personal and focused than group interactions. The intense, unfailing attention of the typical examiner is a rather unusual experience for most people. Being assessed is a break from the examinee’s normal routine, which most examinees find to be quite interesting until the novelty wears off. In addition, the environment is carefully controlled to maximize the examinee’s attention and performance. In other words, the testing is designed to elicit the person’s optimal performance. Therefore, the observed behaviors may not be representative of a person’s typical behaviors in another setting, such as a chaotic home, a noisy classroom, or a competitive work environment.

If you believe that the observed test behaviors are indeed similar to those in the home, school, or workplace, you must confirm that this is the case with supplementary evidence. Direct observation is indispensable, but our best hope for accuracy is in a disciplined, systematic integration of all the available evidence.

Excerpt from pp. 103–104 of Schneider, W. J., Lichtenberger, E. O, Mather, N., & Kaufman, N. L. (2018). Essentials of Assessment Report Writing (2nd ed). Hoboken, NJ: Wiley.

Habitual Hedging Is Unnecessary, Unattractive, and Annoying

To escape criticism—do nothing, say nothing, be nothing.

Elbert Green Hubbard (1909, p. 38)

If you want to be a stickler about it, you can remind people in every statement you make of the deep-seated uncertainty of mortal existence. However, in everyday communication we only introduce doubt when there is reasonable doubt. If you ask a stranger for the time, and he tells you that it is 3:15, you thank him and move along. If he says, “It might be 3:15,” you still thank him, but you look around for someone else with a watch.

In much academic writing, clarity runs a poor second to invulnerability.

Richard Hugo (1992, p. 11)

Expressions of doubt exist for a reason. Suppose someone tells you that Shelby is angry with you. You must decide what to do with that information. Now suppose that someone tells you that Shelby might be angry with you. This information might lead to a different course of action. If the person is quite sure about Shelby’s anger but added “might” because of her philosophical stance that everything is uncertain, she is correct in what she said but incorrect in what she communicated. We rely on social conventions to communicate much that is unstated. If the public is not accustomed to the ways in which we introduce doubt into our sentences, we are miscommunicating. Suppose you write,

Her mother reported that Julia has a “severe peanut allergy.”

You might think the subtext of this sentence is “See how careful I am? I am telling you where I got all my information. Also, I’m not an allergist so it is not my place to say how severe the allergy is. Therefore, I am using Julia’s mother’s words instead of my own.” Many readers will understand that this is all we mean. However, to some readers, we might as well have written,

The “woman” who claims to be Julia’s mother asserted, without evidence, that Julia (if that is indeed her name) has a so-called peanut allergy, which, for reasons unspecified, was described as “severe.”

Why do we write reports with hyper-precise language? We want to be right … and to be respectful. We also want not to be wrong, not to be challenged, and, if we are wrong, not to be responsible. You never know when someone might sue you for saying that an allergy is severe when in fact it is only moderately severe. Steven Pinker (2014) observed,

Writers acquire the hedge habit to conform to the bureaucratic imperative that’s abbreviated as CYA, which I’ll spell out as Cover Your Anatomy. They hope it will get them off the hook, or at least allow them to plead guilty to a lesser charge, should a critic ever try to prove them wrong. …A classic writer counts on the common sense and ordinary charity of his readers, just as in everyday conversation we know when a speaker means “in general” or “all else being equal.” If someone tells you that Liz wants to move out of Seattle because it’s a rainy city, you don’t interpret him as claiming that it rains there twenty-four hours a day seven days a week just because he didn’t qualify his statement with relatively rainy or somewhat rainy. … An adversary who is unscrupulous enough to give the least charitable reading to an unhedged statement will find an opening to attack the writer in a thicket of hedged ones anyway. … It’s not that good writers never hedge their claims. It’s that their hedging is a choice, not a tic. (pp. 44–45)

Let’s start with an excessively hedged statement and then explore some alternatives:

Julia’s mother’s CBCL Externalizing score of 78 suggests that Julia may engage in antisocial behavior more often than her peers.

Suggests? May? These words were no doubt intended as a sign of respect for the uncertainty inherent in the assessment process, but they also reveal an assessment in limbo and only half completed. If the evaluator has no other information about Julia, then, yes, the CBCL Externalizing score does no more than suggest the presence of problems Julia may have. But to stop there means that the evaluator does not understand what rating scales are for.

Rating scales are tools for collecting information efficiently and can focus our investigation on areas of particular concern. However, nothing rating scales can tell us is trustworthy enough to mention in a report—unless it has been corroborated. Once her parents, her teachers, and Julia herself have told us that she has a long history of truancy, shoplifting, and fistfights, the score is beside the point. We base our interpretation on the totality of evidence, not on a particular score. A corroborated score might still tell us something about the rarity of the problem, but to insist on words like suggest bespeaks a perversely cautious epistemology.

The information, interpretations, and conclusions in a classically written report have been thoroughly vetted by the examiner and are verifiable—at least in theory—by anyone. For this reason, they are stated simply, directly, and without hedging. Opinions, predictions, and preferences are clearly labeled as such when necessary, but without compulsive hand-wringing. In this way, the writer shows respect for the reader’s competence in recognizing an opinion for what it is. 

Remove Unnecessary Qualifications and Excessive Sourcing

Statement	Reason for Edit
If Julia’s mother’s recollection is accurate, Julia was born 6 weeks premature.	If anyone is going to be accurate about such a matter, it is going to be Julia’s mother.
According to Julia’s teacher, he gives her extra incentives to stay focused on her seatwork.	There is no reason to doubt Julia’s teacher’s words here. The original wording suggests that Julia’s teacher might have lied, or at best, is confused.
The BASC-3 Self-Report of Personality indicates that Julia possibly has high levels of anxiety.	Rating scales do not have enough authority to stand on their own. Your judgment cannot be outsourced to them. Once the interpretation has been properly confirmed, the reference to the rating scale as a source is superfluous.
Exposure therapy may help Julia manage her debilitating fear of dogs, but it is impossible to know for certain. I recommend exposure therapy to help Julia manage her debilitating fear of dogs.	Almost anything may help Julia. What is your recommendation? There is no need to undermine confidence in your suggestions. It is widely understood that a recommendation is not a guarantee. If you are not ready to make a suggestion you can stand by, your assessment is not yet finished.

At first, the classic style seems overly bold, as if the writers present their opinions as immutable laws. There is legitimate cause for concern here, but the worry is overstated. It is easy to spot the difference between the clear, disinterested pronouncements of classic prose and the bloviation and bluster of pompous windbags. If there is anything that we social creatures are good at, it is recognizing self-promotion, especially when the self-promoter’s interests do not align with our own. Furthermore, there is no set of writing guidelines in the world that will stop pompous windbags from engaging in pompous windbaggery. Therefore, we might as well design our rules of decorum for sensible people of good will.

When there are lingering doubts about the accuracy of a statement in a report, you should gather more evidence until you can say something more definite. No one benefits from words parsed so carefully they are watered down to meaninglessness with mushy maybes, could be sometimes, and possibly some days. These doubt-inducing words are indispensable tools, to be sure, but they are to be used with skill and judgment instead of mechanically inserted in every statement.

Writing in the classic style gives the writer certain license to be clear and direct, but no license for high-handedness. This freedom to be direct in writing is paid for by scrupulous scientific modesty and soul-searching doubt during the assessment phase. Assessment is not a parlor trick in which we guess from minimal information all of the person’s deepest secrets. Rather, we work collaboratively with the person and then verify with all relevant parties whether a possible interpretation is true. Thus, a properly vetted interpretation will come as no surprise when it appears in a report. If despite best efforts, the report is found to have an interpretive error, the report can be amended.

Obviously, hedging is warranted if you expect the report to be included in a lawsuit. If you wish to adopt the classic style, eliminating unnecessary qualification and hedging, but you still want to play it safe, you can include in your report a blanket disclaimer in which you acknowledge the possibility of error and that your observations, conclusions, and recommendations are simply your best guesses rather than claims of absolute certainty.

Excerpt from pp. 37–40 of Schneider, W. J., Lichtenberger, E. O, Mather, N., & Kaufman, N. L. (2018). Essentials of Assessment Report Writing (2nd ed). Hoboken, NJ: Wiley.

Classic Prose Is Simple, Not Simplistic

Simple words, carefully arranged, stick in the memory and influence action long after they have been read. Let us consider three pithy one-liners written by masters of the classic style.

Marie de Rabutin‐Chantal, Madame de Sévigné (1626– 1696)

I fear nothing so much as a man who is witty all day long.

Here Madame de Sévigné jolts us into delightful awareness of a truth we have always felt but never articulated. Furthermore, she has shown us the great honor of trusting us to apply the appropriate scope to her generalization about the dangers of too much wit. To challenge her on her wording—that chronically witty men could not possibly frighten her more than ferocious beasts, incurable disease, and invading soldiers—breaks the spell of her obvious hyperbole and displeases the Madame.

François VI
Duc de La Rochefoucauld
(1613–1680)

The refusal of praise is but the wish to be praised twice.

With maximum efficiency and minimum effort, La Rochefoucauld performs verbal jujitsu on the excessively modest. Stop making yourself the center of attention, he says. Don’t be so awkward about letting people be nice to you. Just thank the person and be done with it.

Blaise Pascal
(1623–1662)

I have made this letter longer than usual because I lack the time to make it shorter.

Pascal’s oft-quoted apology could have been utterly forgettable (e.g., “Sorry about the long letter, but I did not have enough time to edit it properly.”). It achieved immortality because Pascal has skillfully led us to expect one thing and then surprises us with another. In this manner, a rather mundane observation—that editing for brevity is hard—feels fresh and insightful.

These examples of classic prose have a style of humor that does not belong in assessment reports, but they are nevertheless instructive. The three writers have noticed that even qualities that seem unambiguously positive—wit, modesty, and brevity—have hidden dangers, shortcomings, and costs. Assessment professionals, too, see the downsides of certain virtues and the hidden sense in what appear to be self-defeating behaviors. Similar to these masters of classic style, assessment professionals can make messages memorable with surprise, irony, and contrast:

• Daniel is never comfortable, except when he is worrying. Worry helps him plan. Worry keeps him safe. To ask Daniel to stop worrying is to ask him to invite catastrophe.
• Art and Lannie love each other so fiercely that 20 years of quarreling could not tear them apart.
• Although Jackson intimidates other children, he is in some ways more afraid than they are. No one fears the bully more than the bully himself.
• If Gina were more frightened of germs, she would not wash her hands so often. Her skin, rubbed raw from years of constant scrubbing, no longer protects her from infections.
• For many years, procrastination has helped Karla be the productive person she is today. Procrastination may have its downsides, but it has been her partner in combating a worse problem: perfectionism. Her motto is “The task expands to fit the time allotted.” Only looming deadlines have had the power to focus her mind and reshuffle her priorities to work efficiently. Recently, however, this strategy has backfired dramatically …

It would strike the wrong tone if the entire report were ironic in this way, but a few memorable sentences might change a person’s life.

Excerpt from pp. 35–37 of Schneider, W. J., Lichtenberger, E. O, Mather, N., & Kaufman, N. L. (2018). Essentials of Assessment Report Writing (2nd ed). Hoboken, NJ: Wiley.

Why Do Assessment Reports Exist at All?

Think of the time and effort we could save if we simply did our assessments, gathered the relevant parties, and then had an engaging conversation about our findings. Why not let an automated transcript of the conversation serve as the permanent record of the assessment? Abandon all hope, ye who enter here. Even if the practice were feasible, it fundamentally misunderstands the nature of an assessment report.

What a hammer does for the fist, what pliers do for the grip, what a telescope does for the eye, writing does for the mind. Unaided, the mind can contemplate solutions to complex problems, but attention wanders and memories fade. Writing not only preserves our thoughts but also sharpens our thinking. By sequencing sound on durable paper, we can contemplate the products of our own minds from a higher vantage— and with a steady gaze. Our words, now external objects, can be revised, reshaped, refined, reorganized, and most important, revisited. As Susan Sontag (2000) observed, “what I write is smarter than I am. Because I can rewrite it.”

Think of writing not as a way to transmit a message but as a way to grow and cook a message. Writing is a way to end up thinking something you couldn’t have started out thinking. —Peter Elbow (1998, p. 15)

Excerpt from p. 30 of Schneider, W. J., Lichtenberger, E. O, Mather, N., & Kaufman, N. L. (2018). Essentials of Assessment Report Writing (2nd ed). Hoboken, NJ: Wiley.

Making Spirographs in R

I made spiro, an R package for creating animated spirographs. Check it out. I would appreciate any suggestions for improving it.

Spirograph Tutorial

My First Book! Essentials of Assessment Report Writing 2e

It’s official! The second edition of Essentials of Assessment Report Writing has been published. My co-authors and I worked hard to make sure every sentence was worth reading. We hope that our work helps professionals write reports that restore hope and inspire change in the lives of people who have found themselves overwhelmed by circumstance.

I am grateful to Alan and Nadeen Kaufman for the invitation to update and expand upon the first edition and to Liz Lichtenberger, Nancy Mather, and Nadeen Kaufman for welcoming me into their writing team. John Willis and Rita McCleary each contributed a chapter brimming with insight. We selected first-rate scholars and practitioners to contribute examples of great report writing along with annotations that let readers listen in on their report-writing process. Thank you Lisa King Chalukian, Robert Lichtenstein, Linda M. Fishman, Donna Goetz, Elaine Fletcher-Janzen, Christopher J. Nicholls, John M. Garruto, Alison Wilkinson-Smith, Jennie Kaufman Singer, and Susan Engi Raiford.

I wish I were one of those people who write with ease, but for me, every sentence is a wrestling match. I would still be pinned to the mat, with fading hopes of escape if my spouse, Renée Tobin, had not repeatedly made sacrifices in her own full-to-brim schedule to give me the gift of uninterrupted time and solitude. I am forever in awe or her.

A Review of the Receptive, Expressive & Social Communication Assessment—Elementary

The Receptive, Expressive & Social Communication Assessment–Elementary (RESCA-E) is a new and innovative measure of oral language abilities. When its publisher, ATP Assessments, asked me to classify the subtests of the RESCA-E according to their likely loadings on CHC Theory abilities, I billed them for the time it took me to do so. However, I was so impressed with the instrument, I thought that it merited a short review and some statistical investigations of its structure. The review was born of pure enthusiasm–I did not not bill APT Assessments for the many additional hours I spent performing statistical analyses, creating plots, and writing up the results. The review contains several features that cannot be displayed on this blogging platform (e.g., interactive 3D plots), but it can be seen in its entirety here.