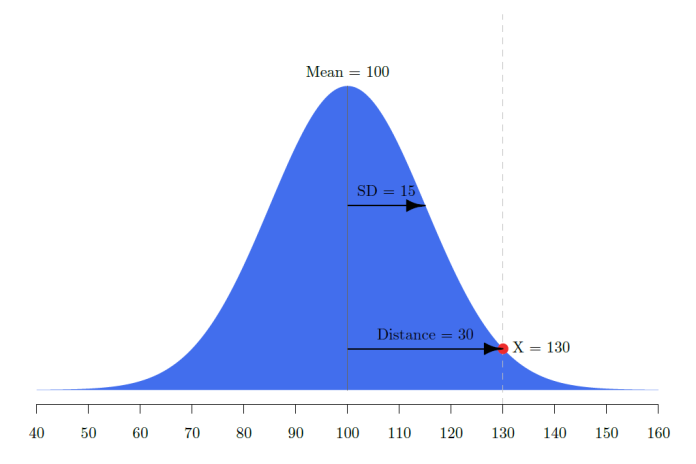
Suppose that two tests have a correlation of 0.6. On both tests an individual obtained an index score of 130, which is 2 standard deviations above the mean. If both tests are combined, what is the composite score?
Our intuition is that if both tests are 130, the composite score is also 130. Unfortunately, taking the average is incorrect. In this example, the composite score is actually 134. How is it possible that the composite is higher than both of the scores?
If I measure the length of a board twice or if I take the temperature of a sick child twice, the average of the results is probably the best estimate of the quantity I am measuring. Why can’t I do this with standard scores?
Standard scores do not behave like many of our most familiar units of measurement. Degrees Celsius have meaning in reference to a standard, the temperature at which water freezes at sea level. In contrast, standard scores do not have meaning compared to some absolute standard. Instead, the meaning of a standard score derives from its position in the population distribution. One way to describe the position of a score is its distance from the population mean. The size of this distance is then compared to the standard deviation, which is how far scores typically are from the population mean (more precisely, the standard deviation is the square root of the average squared distance from the mean). Thus, the “standard” to which standard scores are compared are the mean and standard deviation.
The average of two imperfectly correlated index scores is not an index score. Its standard deviation is smaller than 15 and thus our sense of what index scores mean does not apply to the average of two index scores. To make sense of the composite score, we must convert it into an index score that has a standard deviation of 15.
How is this possible? It is unusual for someone to score 130. It is even more unusual for someone to score 130 on two tests that are imperfectly correlated. The less correlated the tests, the more unusual it is to score high on both tests.
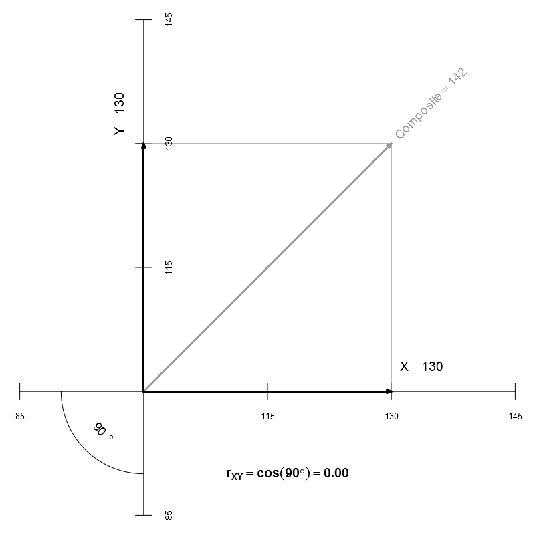
Below is a geometric representation of this phenomenon. Correlated tests can be graphed with oblique axes (as is done in factor analyses with oblique rotations). The cosine of the correlation is the angle between the axes. As seen below, the lower the correlation, the more extreme the composite. As the correlation approaches 1, the composite approaches the average of the scores.
If the scores are lower than the population mean, the composite score is lower than the average of the parts. For example, if the two scores are 71, and the correlation between the scores is 0.9, the composite score is 70.
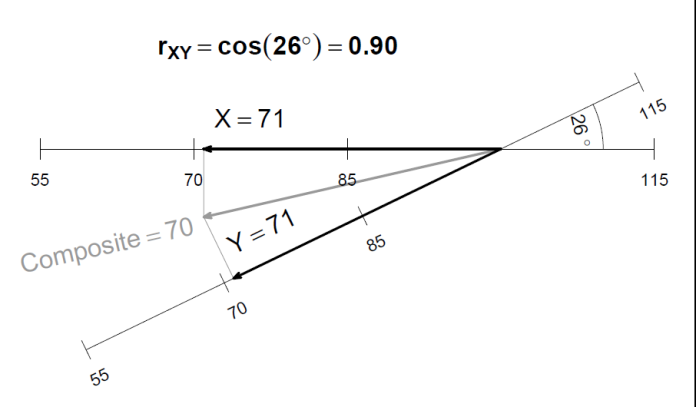
When the subtest scores are below the mean, the composite score is lower than the average of the subtest scores.
In a previous post, I presented this material in greater detail.

Love your website!
Thanks!
Thanks for posting, Joel! This article is SO useful
Glad you liked it!
This is great! Thanks so much for this explanation!
Thanks!
Every time I read a post I become a bigger fan, Joel. Thanks for providing this resource for the rest of us.
Thanks!