Two visualizations for explaining “variance explained”

In my introductory statistics class, I feel uneasy when I have explain what variance explained means. The term has two things I don’t like. First, I don’t like variance very much. I feel much more comfortable with standard deviations. I understand that at a deep level variance is a more fundamental concept than the standard deviation. However, variance is a poor descriptive statistic because there is no direct visual analog for variance in a probability distribution plot. In contrast, the standard deviation illustrates very clearly how much scores typically deviate from the mean. So, variance explained is hard to grasp in part because variance is hard to visualize.

The second thing I don’t like about variance explained is the whole “explained” business. As I mentioned in my last post, variance explained does not actually mean that we have explained anything, at least in a causal sense. That is, it does not imply that we know what is going on. It simply means that we can use one or more variables to predict things more accurately than before.

In many models, if X is correlated with Y, X can be said to “explain” variance in Y even though X does not really cause Y. However, in some situations the term variance explained is accurate in every sense:

X causes Y

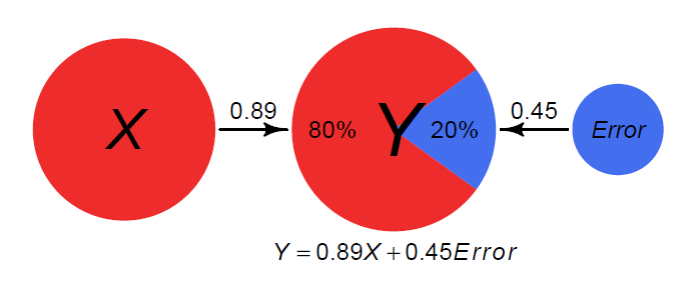
In the model above, the arrow means that X really is a partial cause of Y. Why does Y vary? Because of variability in X, at least in part. In this example, 80% of Y’s variance is due to X, with the remaining variance due to something else (somewhat misleadingly termed error). It is not an “error” in that something is wrong or that someone is making a mistake. It is merely that which causes our predictions of Y to be off. Prediction error is probably not a single variable. It it likely to be the sum total of many influences.

Because X and error are uncorrelated z-scores in this example, the path coefficients are equal to the correlations with Y. Squaring the correlation coefficients yields the variance explained. The coefficients for X and error are actually the square roots of .8 and .2, respectively. Squaring the coefficients tells us that X explains 80% of the variance in Y and error explains the rest.

Visualizing Variance Explained

Okay, if X predicts Y, then the variance explained is equal to the correlation coefficient squared. Unfortunately, this is merely a formula. It does not help us understand what it means. Perhaps this visualization will help:

Variance Explained

If you need to guess every value of Y but you know nothing about Y except that it has a mean of zero, then you should guess zero every time. You’ll be wrong most of the time, but pursuing other strategies will result in even larger errors. The variance of your prediction errors will be equal to the variance of Y. In the picture above, this corresponds to a regression line that passes through the mean of Y and has a slope of zero. No matter what X is, you guess that Y is zero. The squared vertical distance from Y to the line is represented by the translucent squares. The average area of the squares is the variance of Y.

If you happen to know the value of X each time you need to guess what Y will be, then you can use a regression equation to make a better guess. Your prediction of Y is called Y-hat (Ŷ):

When X and Y have the same variance, the slope of the regression line is equal to the correlation coefficient, 0.89. The distance from Ŷ (the predicted value of Y) to the actual value of Y is the prediction error. In the picture above, the variance of the prediction errors (0.2) is the average size of the squares when the slope is equal to the correlation coefficient.

Thus, when X is not used to predict Y, our prediction errors have a variance of 1. When we do use X to predict Y, the average size of the prediction errors shrinks from 1 to 0.2, an 80% reduction. This is what is meant when we say that “X explains 80% of the variance in Y.” It is the proportion by which the variance of the prediction errors shrinks.

An alternate visualization

Suppose that we flip 50 coins and record how many heads there are. We do this over and over. The values we record constitute the variable Y. The number of heads we get each time we flip a coin happens to have a binomial distribution. The mean of a binomial distribution is determined by the probability p of an event occurring on a single trial (i.e., getting a head on a single toss) and the number of events k (i.e., the number of coins thrown). As k increases, the binomial distribution begins to resemble the normal distribution. The probability p of getting a head on any one coin toss is 0.5 and the number of coins k is 50. The mean number of heads over the long run is:

The variance of the binomial distribution:

Before we toss the coins, we should guess that we will toss an average number of heads, 25. We will be wrong much of the time but our prediction errors will be as small as they can be, over the long run. The variance of our prediction errors is equal to the variance of Y, 12.5.

Now suppose that after tossing 80% of our coins (i.e., 40 coins), we count the number of heads. This value is recorded as variable X. The remaining 20% of the coins (10 coins) are then tossed and the total number of heads is counted from all 50 coins. We can use a regression equation to predict Y from X. The intercept will be the mean number of heads from the remaining 10 coins:

In the diagram below, each peg represents a coin toss. If the outcome is heads, the dot moves right. If the outcome is tails, the dot moves left. The purple line represents the probability distribution of Y before any coin has been tossed.

X explains 80% of the variance in Y.

When the dot gets to the red line (after 40 tosses or 80% of the total), we can make a new guess as to what Y is going to be. This conditional distribution is represented by a blue line. The variance of the conditional distribution has a mean equal to Ŷ, with a variance of 2.5 (the variance of the 10 remaining coins).

The variability in Y is caused by the outcomes of 50 coin tosses. If 80% of those coins are the variable X, then X explains 80% of the variance in Y. The remaining 10 coins represent the variability of Y that is not determined by X (i.e., the error term). They determine 20% of the variance in Y.

If X represented only the first 20 of 50 coins, then X would explain 40% of the variance in Y.

 

X explains 40% of the variance in Y.