IQ, the death penalty, and me

Today the Supreme Court of the United States ruled that, in death penalty cases, the state of Florida must take into account the inherent imprecision of IQ tests.

Why are IQ tests used in death penalty cases? It is unconstitutional to execute a person deemed to be intellectually disabled (Intellectual disability is the current term for what was previously known as mental retardation.). Diagnosing intellectual disabilities is a complex matter but the diagnosis hinges to a large degree on the person’s performance on a well-constructed IQ test. Although high-quality IQ tests are more reliable than most psychological measures, even the best IQ tests are imperfectly precise. There is a potentially large risk that a person with an observed score slightly above the threshold set by Florida law may have a “true score” that is below the threshold.

It was an unexpected honor to have my work cited in both the court’s decision (written by Justice Kennedy) and the dissenting opinion (written by Justice Alito). My contribution to the argument (relevant portion reproduced here) is a technical one and played an admittedly small role in the proceedings . My main point was that when multiple IQ tests have been administered to the same individual, we should not average the scores but make them into a composite score in the same way that we combine psychological scores in any other context. Doing so gives a more accurate estimate of the IQ and a smaller confidence interval around the score. I hope that the application of this procedure results in fewer incorrect decisions and a fairer administration of justice.

I am grateful to Cecil Reynolds for giving me the opportunity to write the paper and to Kevin McGrew for encouraging me to re-write and publish the argument on the web, demonstrating its application to death penalty cases. Although it was the published chapter that was cited and used by the defense, it was the free web version that initially caught the attention of the law firm representing the defendant.

Short list of bad things associated with high IQ

IQ is positively correlated with almost everything that is good in life and negatively correlated with almost every bad outcome you can think of. The reasons for these correlations are diverse and often surprising.

Though high IQ is generally associated with positive outcomes, it is associated with a few negative ones. It is unknown how many there are but the list is surely very short. Here are some of them:

1. People with high IQ tend to be nearsighted. The higher the IQ, the more likely the person is going to need glasses. Some stereotypes exist for a reason! Why the association exists is anyone’s guess…and many guesses have been made. The most amusing hypothesis I have found is the idea that big brains squish the eyes! One thing that is clear is that the correlation is not due to excessive reading.
2. People with high IQ tend to have allergies. Another stereotype! However, the evidence for this finding is somewhat mixed. Perhaps there is some sort of trade-off: You can either distinguish between good and bad foreign particles or you can distinguish between good and bad ideas.
3. People with high IQ are more likely to commit suicide? The evidence for this finding is mixed and sometimes in the opposite direction, probably because the relationship IQ and suicide is non-linear and moderated by a number of demographic and cultural factors. My guess is that some people who know that they are talented feel worthless when they have failed to live up to expectations (both their own and other people’s).

A new study suggests that this list might get a little longer (sort of). It is well known that IQ and criminality are negatively correlated and that high IQ appears to be associated with lower levels of criminality even among those otherwise at higher risk of becoming criminals. However, a new study by Hampton, Drabick, and Steinberg suggests that, all else equal, high IQ, among people with psychopathic tendencies, is associated with higher levels of criminal offending.

My interpretation of this is that high cognitive ability is neither good nor bad. Rather, it simply allows you do more of what you want to do. In a well-regulated society in which incentives are properly aligned with good behavior, high intelligence will correlate with good behavior. However, in certain contexts (e.g., criminal organizations and dictatorial regimes), high intelligence amplifies one’s capacity to do harm.

William Stern (1871–1938): The Individual Behind the Intelligence Quotient

Lamiell (1996) notes that if mentioned at all, Stern is known as “the IQ guy,” which in one sense is true enough. He was indeed the one who invented the formula for the intelligence quotient:

What is not typically mentioned is that he was a little embarrassed by his IQ idea and would have been happy if his name were not associated with it (Lamiell, 2003, p. 1). He wrote movingly about how IQ tests should not be used to degrade individuals (Stern, 1933, as cited in Lamiell, 2003):

Under all conditions, human beings are and remain the centers of their own psychological life and their own worth. In other words, they remain persons, even when they are studied and treated from an external perspective with respect to others’ goals….Working “on” a human being must always entail working “for” a human being….The psychotechnician has every good reason to take these considerations seriously. Because if there are places today where the term “psychotechnician” is uttered with something of a disdainful tone, that is due to the implicit or explicit belief that psychotechnicians not only intercede but interfere in the lives and rights of the individuals they deal with. The feeling is that psychotechnicians degrade persons by using them as a means to others’ ends. (pp. 54–55)

Stern wrote extensively about a wide variety of issues about intelligence, personality, individuality, and many other topics. It irked him that the IQ formula was the idea that caught on. Fortunately, scholars are beginning to remember Stern as more than just “The IQ guy.”

Stern’s Humanism & the Limits of Science

Stern used intelligence tests and other scientific approaches to understand people but also wanted to be clear about the limits of such approaches. His work did not constitute a romantic rejection of science but rather a clear-headed delineation of its proper boundaries. In arguably the first book on the psychology of individual differences, Stern (1900, as cited in Lamiell, 2003) provides this thought, which, provided suitably tasteful graphic design, should probably be made into framed posters that psychologists who cherish individuality can hang in their offices:

[E]very individual is a singularity, a one-time existing being, nowhere else and never before present. To be sure, certain law-like regularities apply to him, certain types are embodied in him, but the individual is not exhausted by these laws and types; there remains ever something more, through which the individual is distinct from others who conform to the same laws and types. And this last kernel of being, which reveals the individual to be thus and so, distinct from all others, is not expressible in the language of scientific concepts, it is unclassifiable, incommensurable. In this sense, the individual is a limiting concept, toward which theoretical investigation strives but can never reach; it is, one could say, the asymptote of science. (pp. 15-16)

If a whole poster seems a bit much, “The Individual—The Asymptote Of Science” would fit nicely on a bumper sticker.

Reading Recommendations

Selected publications	Comments
The psychological methods of testing intelligence (Stern, 1914)	Besides showing Stern to be extremely sensible and practical, this book is eye-opening in showing the extremely wide variety of very basic questions that had to be answered before IQ tests could be taken seriously.
William Stern (Stern, 1930)	For those wishing to acquire some intellectual humility, Stern’s autobiography might do the trick. Stern’s prose is at times dense with ideas that at first seem like gibberish but upon close inspection are seen to be quite profound.

References

Lamiell, J. T. (1996). William Stern: More than “the IQ guy.” In G. A. Kimble, C. Alan Boneau, & M. Wertheimer (Eds.), Portraits of pioneers in psychology, Vol. II, pp. 73–85. Hillsdale, NJ: Erlbaum.

Lamiell, J. T. (2003). Beyond individual and group differences: Human individuality, scientific psychology, and William Stern’s critical personalism. Thousand Oaks, CA: Sage.

Stern, W. (1900). Über Psychologie der individuellen Differenzen (Ideen zu einer “Differentiellen Psychologie”) [On the psychology of individual differences (Toward a “differential psychology”)]. Leipzig: Barth.

Stern, W. (1914). The psychological methods of testing intelligence (G. M. Whipple, Trans.). Baltimore: Warwick & York. (Original work published 1912)

Stern. W. (1930). William Stern. In C. Murchinson (Ed.), A history of psychology in autobiography, (Vol. 1, pp. 335-388). New York: Russell & Russell,

Stern, W. (1933). Der personale Faktor in Psychotechnik und praktischer Psychologie [The personal factor in psychotechnics in practical psychology]. Zeitschrift für angewandte Psychologie, 44, 52–63.

Why averaging multiple IQ scores is incorrect in death penalty cases

As I have explained elsewhere on this blog, when a person has been given multiple IQ tests, it is common practice to take the mean IQ or median IQ to determine eligibility for the death penalty. As long as all the scores are valid estimates, combining multiple scores results in more accurate measurement.

Unfortunately, taking the mean or median IQ score is one of those solutions that is simple, neat, and wrong. Why? In the graph below, there are two IQ tests that correlate at 0.9. On each test, the population mean is μ = 100 and the standard deviation is σ = 15. On either test alone, about 2.3% of people score 70 or less, the typical threshold at which a person is ineligible for the death penalty.

What percent of people score 70 or less on the average of the 2 tests? About 2%. Why is it 2% instead of 2.3%? The smaller number occurs because the tests, though highly correlated, are not perfectly correlated. The average of the 2 tests has a population mean of μ = 100 but its standard deviation is smaller than 15. In this case, the standard deviation is σ = 14.62. The fact that the standard deviation of the average of two scores is smaller results in fewer people below the threshold of 70 than is the case if just one test had been given.

There is an established procedure for rescaling a composite score so that it has the correct mean and standard deviation. It is the same procedure that was applied to the IQ subtest scores in the calculation of the full scale IQ. This same procedure should be applied when multiple IQ scores have been given.

Assuming that all the IQ scores have a mean of μ = 100 and a standard deviation of σ = 15, the composite IQ of k scores is:

In the graph above, the diagonal axis represents the composite IQ with the proper scaling so that the composite IQ has a mean of 100 and a standard deviation of 15 (instead of 14.62). As stated previously, if the 2 IQ tests were simply averaged, only about 2.0% score 70 or less. On a properly scaled IQ score, 2.0% corresponds to an IQ of 69.

Does 1 point matter? It does to the person who on average scored 71 on the 2 IQ tests. That person, with the score properly rescaled, would have a composite IQ of  70 and thus would be deemed ineligible for execution.

Your intuition might be telling you that something is fishy about all this. Does this mean that whenever someone scores 71 on an IQ test, just missing the threshold, that another test should be given, resulting in another score of 71 so that the composite score is 70? The answer is that your intuition (and mine) is often unreliable when it comes to probability. As I have explained in this video, most people who score 71 on one IQ test score higher than 71 on a second IQ test. As long as all the scores are properly rescaled, the composite IQ is more accurate and nothing fishy is happening.

This procedure should not be applied mechanically in all situations. The method assumes that each score is equally valid and thus has equal weight. There are reasons to prefer some IQ administrations over others (e.g., a full battery given by a licensed clinician is likely to be more accurate than an abbreviated IQ test given by a first-year graduate student). If there are reasons to dismiss a particular score (e.g., the evaluee intentionally tried to obtain a low score), it should not figure into the composite score. There are further complications not discussed here such as the fact that people tend to score higher when retested with the same test (or one that is very similar).

g Factor Removed from Correlation Matrices, Vizualized

As a follow up to yesterday’s post, I extracted a g factor from the matrix of each battery and made these pictures of the residual matrices. I filtered out all the negative residuals to de-clutter the image.

I am not sure what can be learned from such pictures other than getting a sense of the magnitudes of the the differences in strength of the different factors. You can see that Gc is generally much stronger than the other factors (except in the case of the SB5).

Correlation Matrices from Five Cognitive Ability Tests, Visualized

Sometimes it is interesting to look at something familiar in a new way. Here are the correlations among the subtests of five major cognitive ability batteries (data comes from the standardization samples). Stronger correlations are thicker and darker. What do you see?

Figures made with semPlot.

Note that color schemes across batteries are not theoretically consistent.

Why do IQ tests measure vocabulary?

If Lexical Knowledge (understanding of words and their uses) is simply memorizing the definitions of fancy words, then, at best, it is a trivial ability valued by academics, pedants, and fuddy-duddies. At worst, its elevation by elitists is a tool of oppression. There is some truth to these views of Lexical Knowledge but they are myopic. I will argue that vocabulary tests are rightfully at the center of most assessments of language and crystallized intelligence. Some words have the power to open up new vistas of human experience. For example, when I was thirteen, learning the word “ambivalence” clarified many aspects of interpersonal relationships that were previously baffling.

A word is an abstraction. The need for labels of simple categories is perfectly clear. Knowing the word anger (or its equivalent in any other language) frees us from having to treat each encounter with the emotion as a unique experience. Being able to communicate with others about this abstract category of experience facilitates self-awareness and the understanding of interpersonal relations. We can build up a knowledge base of the sorts of things that typically make people angry and the kinds of reactions to expect from angry people.

It is less obvious why anger has so many synonyms and near-synonyms, some of which are a bit obscure (e.g., iracund, furibund, and zowerswopped!). Would it not be easier to communicate if there were just one word for every concept? It is worthwhile to consider the question of why words are invented. At some point in the history of a language, a person thought that it would be important to distinguish one category of experience from others and that this distinction merited a single word. Although most neologisms are outlived even by their inventors, a few of them are so useful that they catch on and are used by enough people for enough time that they are considered “official words” and are then taken for granted as if they had always existed.[1] That is, people do not adopt new words with the primary goal of impressing one another. They do it because the word succinctly captures an idea or a distinction that would otherwise be difficult or tiresome to describe indirectly. Rather than saying, “Because Shelly became suddenly angry, her sympathetic nervous system directed her blood away from her extremities toward her large muscles. One highly visible consequence of this redirection of blood flow was that her face turned white for a moment and then became discolored with splotches of red.” It is simply more economical to say that “Shelly was livid with rage.” By convention, the use of the word livid signals that Shelly is probably not thinking too clearly at the moment and that the next thing that Shelly says or does is probably going to be impulsive and possibly hurtful.

Using near synonyms interchangeably is not merely offensive to word nerds and the grammar police. It reflects, and possibly leads to, an impoverishment of thought and a less nuanced understanding of the world. For example, jealousy is often used as a substitute for envy. They are clearly related words but they are not at all the same. In fact, in a sense, they tend to be experienced by people on opposite sides of a conflicted relationship. Envy is the painful, angry awareness that someone else enjoys some (probably undeserved) advantage that we covet. Jealousy is the angry, often vigilant, suspicion we may lose our beloved to a rival. Unaware of this distinction, it would be difficult to benefit from or even make sense of the wisdom of Rochefoucauld’s observation that “Jealousy is born with love, but does not die with it.”

Lexical Knowledge is obviously important for reading decoding. If you are familiar with a word, it is easier to decode. It is also obviously important for reading comprehension. If you know what a word means, it is easier to comprehend the sentences in which it appears. It is probably the case that reading comprehension also influences Lexical Knowledge. Children who comprehend what they read are more likely to enjoy reading and thus read more. Children who read more expose themselves to words that rarely occur in casual speech but the meaning of which can be inferred from how it is used in the text. Finally, Lexical Knowledge is important for writing. Children with a rich understanding of the distinctions between words will not only be able to express what they mean more precisely, but their knowledge of certain words will enable them to express thoughts that they might not otherwise have had. For example, it seems to me unlikely that a student unfamiliar with the word “paradox” would be able to write an essay about two ideas that appear to be contradictory at first glance but at a deeper level are consistent with each other.

---

[1] Of course, dictionaries abound with antique words that were useful for a time but now languish in obscurity. For example, in our more egalitarian age, calling someone a cur (an inferior dog because it is of mixed breed) is not the insult that it once was. It is now used mostly for comedic effect when someone affects an aristocratic air. My favorite example of a possibly soon-to-be antique word is decadent, which is nowadays almost exclusively associated with chocolate.

This post is an excerpt from:

Schneider, W. J. (2013). Principles of assessment of aptitude and achievement. In D. Saklofske, C. Reynolds, & V. Schwean (Eds.), Oxford handbook of psychological assessment of children and adolescents (pp. 286–330). New York: Oxford.

Can’t Decide Which IQ Is Best? Make a Composite Score.

A man with a watch knows what time it is. A man with two watches is never sure.

-Segal’s Law

Suppose you have been asked to settle a matter with important implications for an evaluee.[1] A young girl was diagnosed with mental retardation [now called intellectual disability] three years ago. Along with low adaptive functioning, her Full Scale IQ was a 68, two points under the traditional line used to diagnose [intellectual disability]. Upon re-evaluation two months ago, her IQ, derived from a different test, was now 78. Worried that their daughter would no longer qualify for services, the family paid out of pocket to have their daughter evaluated by another psychologist and the IQ came out as 66. Because of your reputation for being fair-minded and knowledgeable, you have been asked to decide which, if any, is the real IQ. Of course, there is no such thing as a “real IQ” but you understand what the referral question is.

You give a different battery of tests and the girl scores a 76. Now what should be done? It would be tempting to assume that, “Other psychologists are sloppy, whereas my results are free of error.” However, you are fair minded. You know that all scores have measurement error and you plot the scores and their 95% confidence intervals as seen in Figure 1.

Figure 1

Recent IQ Scores and their 95% Confidence Intervals from the Same Individual

It is clear that Test C’s confidence interval does not overlap with those of Tests B and D. Is this kind of variability in scores unusual?[2] There are two tests that indicate an IQ in the high 60’s and two tests that indicate an IQ in the high 70’s. Which pair of tests is correct? Should the poor girl be subjected to yet another test that might act as a tie breaker?

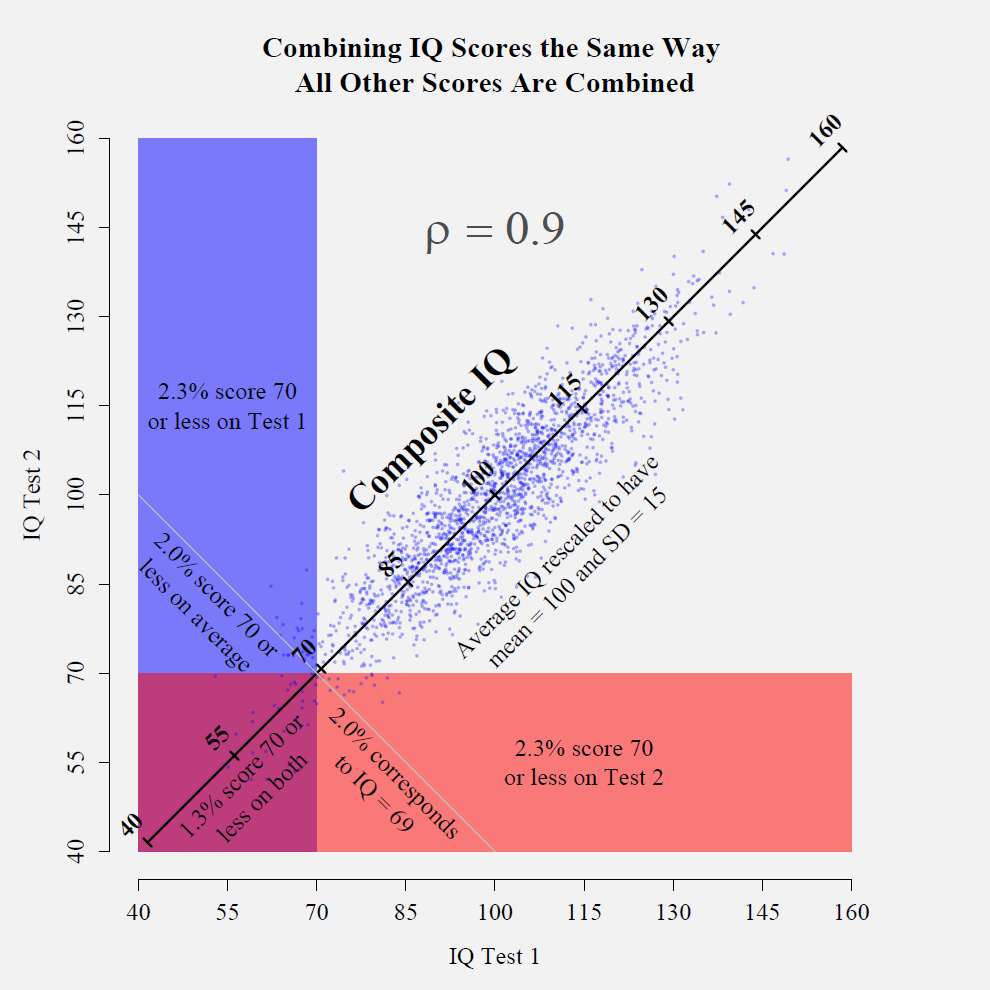
Perhaps the fairest solution is to treat each IQ test as subtests of a much larger “Mega-IQ Test.” That is, perhaps the best that can be done is to combine the four IQ scores into a single score and then construct a confidence interval around it.

Where should the confidence interval be centered? Intuitively, it might seem reasonable to simply average all four IQ results and say that the IQ is 72. However, this is not quite right. Averaging scores gives a rough approximation of a composite score but it is less accurate for low and high scorers than it is for scorers near the mean. An individual’s composite score is further away from the population mean than the average of the individual’s subtest scores. About 3.1% of people score a 72 or lower on a single IQ test (assuming perfect normality). However, if we were to imagine a population of people who took all four IQ tests in question, only 1.9% of them would have an average score of 72 or lower. That is, it is more unusual to have a mean IQ of 72 than it is to score a 72 IQ on any particular IQ test. It is unusual to score 72 on one IQ test but it is even more unusual to score that low on more than one test on average. Another way to think about this issue is to recognize that the mean score cannot be interpreted as an IQ score because it has a smaller standard deviation than IQ scores have. To make it comparable to IQ, it needs to be rescaled so that it has a “standard” standard deviation of 15.

Here is a good method for computing a composite score and its accompanying 95% confidence interval. It is not nearly as complicated as it might seem at first glance. This method assumes that you know the reliability coefficients of all the scores and you know all the correlations between the scores. All scores must be index scores (μ = 100, σ = 15). If they are not, they can be converted using this formula:

Computing a Composite Score

Step 1: Add up all of the scores.

In this case,

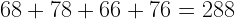
Step 2: Subtract the number of tests times 100.

In this case there are 4 tests. Thus,

Step 3: Divide by the square root of the sum of all the elements in the correlation matrix.

In this case, suppose that the four tests are correlated as such:

	Test A	Test B	Test C	Test D
Test A	1	0.80	0.75	0.85
Test B	0.80	1	0.70	0.71
Test C	0.75	0.70	1	0.78
Test D	0.85	0.71	0.78	1

The sum of all 16 elements, including the ones in the diagonal is 13.18. The square root of 13.18 is about 3.63. Thus,

Step 4: Complete the computation of the composite score by adding 100.

In this case,

Given the four IQ scores available, assuming that there is no reason to favor one above the others, the best estimate is that her IQ is 69. Most of the time, there is no need for further calculation. However, we might like to know how precise this estimate is by constructing a 95% confidence interval around this score.

Confidence Intervals of Composite Scores

Calculating a 95% confidence interval is more complicated than the calculations above but not overly so.

Step 1: Calculate the composite reliability.

Step 1a: Subtract the number of tests from the sum of the correlation matrix.

In this case, there are 4 tests. Therefore,

Step 1b: Add in all the test reliability coefficients.

In this case, suppose that the four reliability coefficients are 0.97, 0.96, 0.98, and 0.97. Therefore,

Step 1c: Divide by the original sum of the correlation matrix.

In this case,

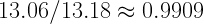
Therefore, in this case, the reliability coefficient of the composite score is higher than that of any single IQ score. This makes sense, given that we have four scores, we should know what her IQ is with greater precision than we would if we only had one score.

Step 2: Calculate the standard error of the estimate by subtracting the reliability coefficient squared from the reliability coefficient and taking the square root. Then, multiply by the standard deviation, 15.

In this case,

Step 3: Calculate the 95% margin of error by multiplying the standard error of the estimate by 1.96.

In this case,

The value 1.96 is the approximate z-score associated with the 95% confidence interval. If you want the z-score associated with a different margin of error, then use the following Excel formula. Shown here is the calculation of the z-score for a 99% confidence interval:

Step 4: Calculate the estimated true score by subtracting 100 from the composite score, multiplying the reliability coefficient, and adding 100. That is,

In this case,

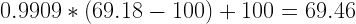
Step 5: Calculate the upper and lower bounds of the 95% confidence interval by starting with the estimated true score and then adding and subtracting the margin of error.

In this case,

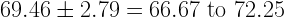
This means that we are 95% sure that her IQ is between about 67 and 72. Assuming that other criteria for mental retardation [intellectual disability] are met, this is in the range to qualify for services in most states. It should be noted that this procedure can be used for any kind of composite score, not just for IQ tests.

---

[1] An Excel spreadsheet I wrote can calculate all of the statistics in this section and can be downloaded for free at http://my.ilstu.edu/~wjschne/AssessingPsyche/AssessingPsycheSoftware.html.

[2] This degree of profile variability is not at all unusual. In fact, it is quite typical. A statistic called the Mahalanobis Distance (Crawford & Allen, 1994) can be used to estimate how typical an individual profile of scores is compared to a particular population of score profiles. Using the given correlation matrix and assuming multivariate normality, this profile is at the 86^th percentile in terms of profile unusualness…and almost of all of the reason that it is unusual is that its overall elevation is unusually low (Mean = 72). If we consider only those profiles that have an average score of 72, this profile’s unusualness is at the 54^th percentile (Schneider, in preparation). That is, the amount of variability in this profile is typical compared to other profiles with an average score of 72.

This post is an excerpt from:

Schneider, W. J. (2013). Principles of assessment of aptitude and achievement. In D. Saklofske, C. Reynolds, & V. Schwean (Eds.), Oxford handbook of psychological assessment of children and adolescents (pp. 286–330). New York: Oxford.

Figure 1 was updated from the original to show more accurately the precision that IQ scores have.

Predicted Achievement Using Simple Linear Regression

There are two ways to make an estimate of a person’s abilities. A point estimate (a single number) is precise but usually wrong, whereas an interval estimate (a range of numbers) is usually right but can be so wide that it is nearly useless. Confidence intervals combine both types of estimates in order to balance the weaknesses of one type of estimate with the strengths of the other. If I say that Suzie’s expected reading comprehension is 85 ± 11, the 85 is the point estimate (also known as the expected score or the predicted score or just Ŷ). The ± 11 is called the margin of error. If the confidence level is left unspecified, by convention we mean the 95% margin of error. If I add 11 and subtract 11 to get a range from 74 to 96, I have the respective lower and upper bounds of the 95% confidence interval.

Calculating the Predicted Achievement Score

I will assume that both the IQ and achievement scores are index scores (μ = 100, σ = 15) to make things simple. The predicted achievement score is a point estimate. It represents the best guess we can make in the absence of other information. The equation below is called a regression equation.

If X is IQ, Y is Achievement, and both scores are index scores (μ = 100, σ = 15), the regression equation simplifies to:

Predicted achievement = (Correlation between IQ and Achievement) (IQ – 100) + 100

Calculating the Confidence Interval for the Predicted Achievement Score

Whenever you make a prediction using regression, your estimate is not exactly right very often. It is expected to differ from the actual achievement score by a certain amount (on average). This amount is called the standard error of the estimate. It is the standard deviation of all the prediction errors. Thus, it is the standard to which all the errors in your estimates are compared. When both scores are index scores, the formula is

To calculate the margin of error, multiply the standard error of the estimate by the z-score that corresponds to the degree of confidence desired. In Microsoft Excel the formula for the z-score corresponding to the 95% confidence interval is

=NORMSINV(1-(1-0.95)/2)

≈1.96

For the 95% confidence interval, multiply the standard error of the estimate by 1.96. The 95% confidence interval’s formula is

95% Confidence Interval = Predicted achievement ± 1.96 * Standard error of the estimate

This interval estimates the achievement score for 95% of people with the same IQ as the child. About 2.5% will score lower than this estimate and 2.5% will score higher.

You can use Excel to estimate how unusual it is for an observed achievement score to differ from a predicted achievement score in a particular direction by using this formula,

=NORMSDIST(-1*ABS(Observed-Predicted)/(Standard error of the estimate))

If a child’s observed achievement score is unusually low, it does not automatically mean that the child has a learning disorder. Many other things need to be checked before that diagnosis can be considered valid. However, it does mean that an explanation for the unusually low achievement score should be sought.

This post is an excerpt from:

Schneider, W. J. (2013). Principles of assessment of aptitude and achievement. In D. Saklofske, C. Reynolds, & V. Schwean (Eds.), Oxford handbook of psychological assessment of children and adolescents (pp. 286–330). New York: Oxford

Potential Misconceptions about Potential

          If you are a mono-g-ist, you can use the estimate of g (IQ) to get an idea of what is the typical range of achievement scores for a child with that IQ. Not every child with the same IQ will have the same achievement scores.[1] Not even mono-g-ists believe that. Also, it is simply not true that achievement cannot be higher than IQ. Equally false is the assumption that if achievement is higher than IQ, then the IQ is wrong. These misconceptions are based on two premises: one true, the other false. If potential is the range of all possible outcomes, it is logically true that people cannot exceed their potentials. The false premise is that IQ and achievement tests are measured on the “potential scale.” By analogy, if I say, “This thermometer reads -10 degrees. I know from my understanding of physics that Brownian motion never stops and thus no temperature dips below zero. Therefore, this thermometer is incorrect.” My premise is true, if the thermometer is on the Kelvin scale. However, it is on the Celsius scale and so there is no reason to believe that something is amiss. IQ and achievement simply are not measured on the “potential scale.” They are measured with standard scores, which are transformed deviations from a population mean. Because of this about half of all people have academic achievement scores that are higher than their own IQ. There is nothing wrong with this.

---

[1] And not every child with the same achievement scores will have the same IQ.

This post is an excerpt from:

Schneider, W. J. (2013). Principles of assessment of aptitude and achievement. In D. Saklofske, C. Reynolds, & V. Schwean (Eds.), Oxford handbook of psychological assessment of children and adolescents (pp. 286–330). New York: Oxford